大數據說話，疫苗有效率嚴重造假！

作者： 同根 無弦 古金

當今很多科研論文和報告，對新冠疫苗的真實有效率，千方百計地掩蓋，並且隱藏關鍵的數據，讓你無法計算或檢驗。這些新近的文獻中，有的提供的數據多一點，我們可以結合大數據算出疫苗整體有效率——不僅僅是不合格

一些病例接種新冠疫苗後出現罕見腦部疾病——朊病毒病（prion disease），而且死亡率極高

（接上篇）

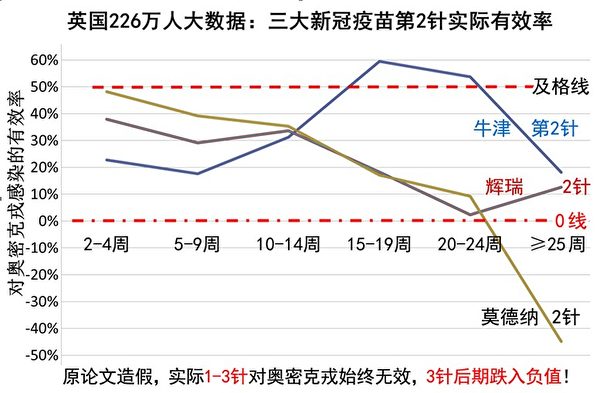
圖5：英論文266萬人大數據糾正後的疫苗第2針有效率圖

上一篇，我們結合大數據計算，揭示了英國和澳洲的4份新冠疫情研究統計報告，有意掩蓋負值有效率，為疫苗洗地。那些造假並非個案，也絕非我們在《大數據否定新冠疫苗防重症》中列舉的那一點。

當今很多科研論文和報告，對新冠疫苗的真實有效率，千方百計地掩蓋，並且隱藏關鍵的數據，讓你無法計算或檢驗。這些新近的文獻中，有的提供的數據多一點，我們可以結合大數據算出疫苗整體有效率——不僅僅是不合格(<50%)，絕大部分跌入負值。

負值有效率表明疫苗有反作用，促進感染、重症、死亡，這是ADE效應的明證。一旦突變出「重症」病毒，ADE就可能會對人類形成大規模的絞殺，可是人類卻像被無形之手操控了一樣，在全面推進它……

5.美國麻省報告，掩藏有效率-60%

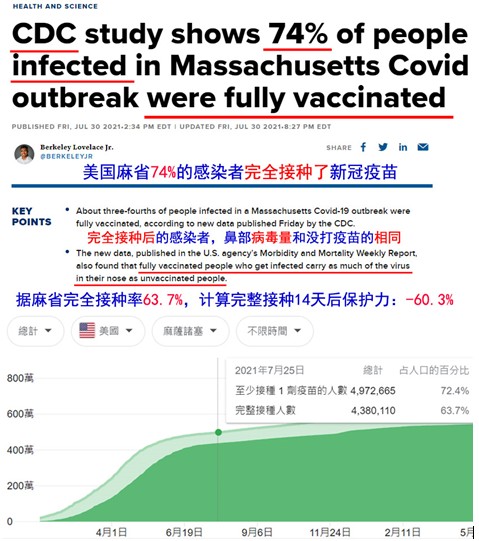
圖6：美國麻省2021年7月的數據，隱藏了疫苗的負值有效率

上面的新聞報導：美國麻省感染者74%完全接種了（一般是2針）疫苗，本該引起對疫苗無效的廣泛關注，但是並沒有，專家和媒體淡化處理——因為並沒擊中要害，74%不能直接說明問題，關鍵要看有效率。

該新聞源自2021年7月的一篇論文[1]，是對美國麻省巴恩斯特布爾縣疫情的大數據報告，隱藏了關鍵的有效率。該文只對病例做了「完全接種疫苗」和「非完全接種疫苗」的區分。因為麻省的疫苗接種率，最接近該縣的情況，故以麻省接種率來計算。

表10：巴恩斯特布爾縣7月感染及麻省接種率

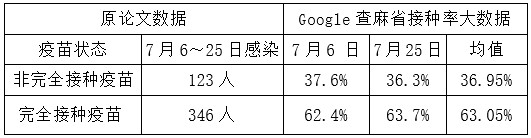
Ve=1-(346/63.7%)/(123/36.3%)=-60.3%

以均值接種率校正：Ve=1-(346/63.05%)/(123/36.95%)=-64.9%

再次證明：2針疫苗促進感染，起反作用！

6.英國49周報告，三證疫苗促進死亡

根據英國新冠病毒49周報告[2]中「打疫苗60天內致死率」的數據，結合查到的大數據接種率：

表11：英國2021.11.8～12.5新冠病毒死亡與疫苗接種率

可算得2針疫苗對60天內死亡的保護率：

Ve=1-(3163/68.75%)/(816/24.55%)=-38.4%

負值又現，2針新冠疫苗促進死亡！

7.蘇格蘭12月報告，四證疫苗促進死亡

(1)掩蓋疫苗有效率

蘇格蘭2021.10.23～11.19的新冠疫情報告[3]，手法和上篇講述的「掩蓋技巧」如出一轍，只不過是以「死亡率」來掩藏有效率負值——畢竟負值有效率太丟人！而他們的「死亡率數據組」有問題，被統一「處理」過，後文會揭示。

圖7：蘇格蘭報告疫情死亡人數表，以死亡率掩蓋疫苗的「負值有效率」。

(2)大數據計算疫苗整體有效率

衡量疫苗是否有用，要計算「疫苗有效率」，計算公式不受上圖紅框中「有問題的數字」的干擾。查證蘇格蘭疫苗接種率，真實有效率如下：

Ve(10.23～29)=1-(110/71.50%)/(14/21.00%)=-130.77%，其它省略計算過程，結果見下表。

表12：大數據計算的疫苗保護率（蘇格蘭43-46周）

(3)與傳統有效率計算對比

上述報告提供的原始數據較多，可以用常規方法計算實際有效率，作為對比。

表13：蘇格蘭第二針疫苗有效率，兩種計算方法對比

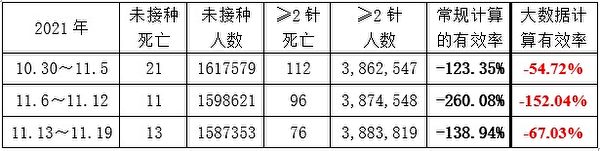
對比可見，大數據計算的有效率，比實際偏高一半左右。畢竟上面未接種組死亡人數少（儘管樣本每周都是540萬人以上的總數），可能出現偏差，需要進一步檢驗。

8.「大數據有效率算法」的進一步檢驗

(1)偏差的由來：傾向性的「科研分組」

表14：當今傾向性的疫苗「科研分組」方法

新冠疫苗的「科研分組」建立在3個假設基礎上：

①假設第1針疫苗21天後才有效，因為那時抗體才多；

②假設第2針疫苗14天後才有效，因為那時抗體才多；

③假設有效抗體多，就能抗病毒（錯！因為舊抗體不抗變異後的新病毒，抗體可能起ADE反作用）。

前兩個假設，已被前面大數據計算的很多疫苗有效率負值所反證，可見這樣分組的前提就錯了。

(2)「大數據算法」：借用「科研分組」和「統計分組」，4點抬高有效率

圖8：本文大數據計算疫苗有效率的公式

1）表14「未合法接種組」包括：

①沒打疫苗的；

②打1針疫苗不到21天的（更容易染疫）；

③打後21天內沒做好防護，暴露在病毒環境中的——這個很難做到，誰能保證自己接觸的環境中沒有病毒呢？所以實際操作中，這一標準搞成了「打1針後21天內感染病毒」。

這樣，人為增大了本組病例，公式中「N病」變大了，抬高了Ve值。

2）表14「完全接種組」剔除：

①打第2針不到14天的（更容易染疫）；

②打第2針14內沒防護好，暴露在病毒環境中的——這個同樣難做，所以實際操作成了「打第2針後14天內感染的」。

這樣人為減少了本組病例，公式中「Y病」變小了，再次抬高了Ve值。

3）大數據查的「Y率」相對大：

大數據查的數據不是「科研分組」，而是「統計分組」。它的「總人口2針接種率」，可不管你是否14天，打了兩針就算，所以公式中「Y率」的值相對大，又抬高了Ve值。

4）大數據查的「N率」相對小：

同樣，大數據查的未接種率相對小，不包括打1針不到21天的人，和打1針21天內染疫的人，「N率」相對變小了，第4次抬高了Ve。

所以，在查不到內部藏而不露的數據的情況下，只能用上述「大數據算法公式」計算時，會高估疫苗2針及以上針的有效率。

(3)「大數據算法」：實際檢驗偏高——如此高估還不行，疫苗更無效

以2021年12月1日出版的蘇格蘭公衛疫情統計報告[4]為例，下面四周的數據，每周的研究都是基於580多萬人的大數據。

以第一周為例，以原文數據，計算≥2針對感染的保護率：

Ve=1-(10795/3862547)/(6930/1617579)=34.76%

以google大數據查到的蘇格蘭接種率，計算2針對感染的保護率：

Ve=1-(10795/71.70%)/(6930/20.80%)=54.81%（其它計算過程略）

表15：蘇格蘭2021.10.30～11.26報告計算常規有效率和「大數據計算有效率」對比

對比可見，大數據計算有效率同樣都偏高，和我們的理論預期一致。在本例要高一半左右，和上文的偏高程度（對死亡的保護率）一致。

所以，如果「大數據計算的有效率」還不合格的話，就更能說明疫苗不合格了。在原始數據被掩藏、不足以校驗有效率真偽的情況下，不失為一種有效的辦法——下表的結果也正是這樣。

表16：大數據計算的新冠疫苗有效率簡表

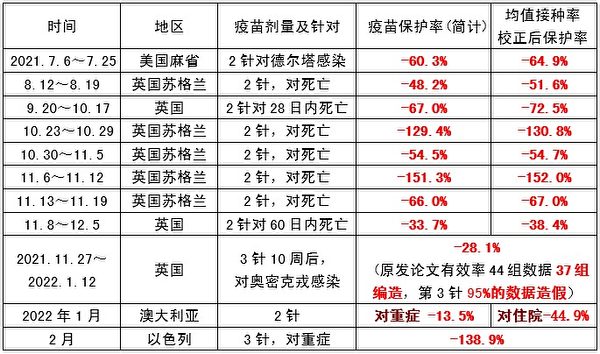
在下篇，我們會建立數學模型，作為判定疫苗有效率真假的試金石。

（未完，待續）

[1] Brown CM, et al. Outbreak of SARS-CoV-2 Infections, Including COVID-19 Vaccine Breakthrough Infections, Associated with Large Public Gatherings— Barnstable County, Massachusetts, July2021. MMWR Morb Mortal Wkly Rep2021;70:1059-1062. DOI:10.15585/mmwr.mm7031e2

[2] COVID-19 vaccine surveillance report Week49，UK Health Security Agency

[3] Public Health Scotland COVID-19 Statistical Report As at29 November2021,Publication date:01 December2021,Public Health Scotland

[4] Public Health Scotland COVID-19 Statistical Report As at29 November2021,Publication date:01 December2021,Public Health Scotland

責任編輯： 江一 　

來源：大紀元 - abolowang